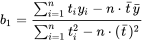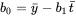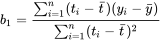RiverMao

从未来再见

线性最小二乘法的参数解

2023-03-02

定义

最小二乘法（英语：least squares method），又称最小平方法，是一种数学优化建模方法。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便的求得未知的数据，并使得求得的数据与实际数据之间误差的平方和为最小。

“最小二乘法”是对线性方程组，即方程个数比未知数更多的方程组，以回归分析求得近似解的标准方法。

最小二乘所涵义的最佳拟合，即残差（残差为：观测值与模型提供的拟合值之间的差距）平方总和的最小化。

最小二乘法分为两种:线性(普通)最小二乘法 和 非线性最小二乘法。

示例

现在对某次实验获取的数据:svg.image?(x,y) :(1,6) (2,5) (3,7) (4,10)使用最小二乘法进行线性拟合。设这条直线为: svg.image?y=\beta_{1}+\beta_{2}x

将四个点代入直线方程中:

svg.image?\left\{\begin{matrix}%206=\beta_{1}+1\beta_{2}\\%205=\beta_{1}+2\beta_{2}\\%207=\beta_{1}+3\beta_{2}\\%2010=\beta_{1}+4\beta_{2}\\\end{matrix}\right.

根据最小二乘法的定义,我们尽量要求等号两边的平方差最小:

即找出:

svg.image?S(\beta1,\beta2)=&space;(6-(\beta_{1}+1\beta_{2}))^{2}+(5-(\beta_{1}+2\beta_{2}))^{2}+(7-(\beta_{1}+3\beta_{2}))^{2}+(10-(\beta_{1}+4\beta_{2}))^{2}

函数的最小值。

可以对svg.image?\inline%20S(\beta1,\beta2)分别求svg.image?\inline%20\beta1和svg.image?\inline%20\beta2的偏导,然后使他们等于零得到:

svg.image?\left\{\begin{matrix}&space;\frac{\partial&space;S}{\partial&space;\beta_{1}}=0=8\beta_{1}+20\beta_{2}-56&space;\\\\&space;\frac{\partial&space;S}{\partial&space;\beta_{2}}=0=20\beta_{1}+60\beta_{2}-154&space;\\\end{matrix}\right.

对此二元一次方程组可求得解为:

svg.image?\left\{\begin{matrix}\beta_{1}&space;=&space;3.5&space;\\\beta_{2}&space;&space;=&space;1.4&space;\\\end{matrix}\right.

即这条直线为:

svg.image?y=3.5+1.4x

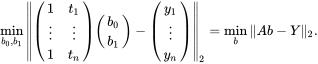
针对线性模型的参数解

对于一条任意的线性拟合方程:

png.image?\dpi{110}y=b_{0}%20+b_{1}t

针对最小二乘法的定义,可以列出矩阵式:

vjnKyD.png

跟上文示例中的方法类似,继续分别求png.image?\dpi{110}b_{0}和png.image?\dpi{110}b_{1}的偏导即可,此处不再赘述,直接给出参数解:

vjuEng.png

vjukjS.png

其中 png.image?\dpi{110}\overline{t} 为 png.image?\dpi{110}t 值的算术平均数,也可以对png.image?\dpi{110}b_{1}的解写为如下形式:

vjuTbQ.png